Understanding the Equation for Axis of Symmetry
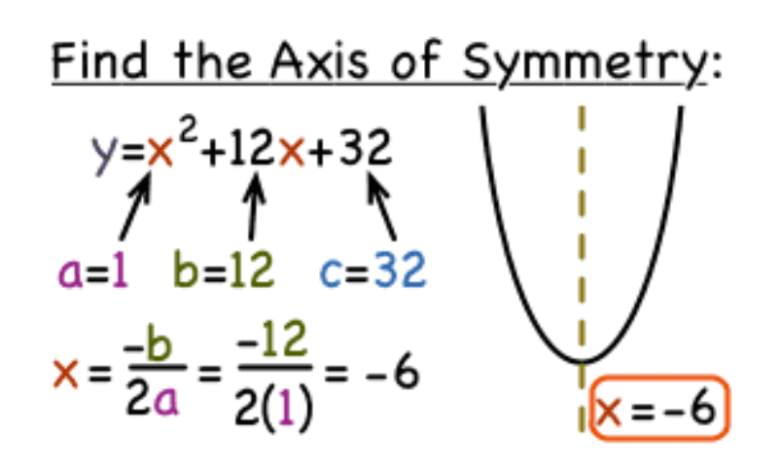
Introduction
In mathematics, especially when studying quadratic functions, the concept of symmetry plays a crucial role. This line is known as the axis of symmetry, and understanding how to find its equation is key to graphing and analyzing quadratic functions. But what is the equation for axis of symmetry and how is it used in problem-solving?
This article explores the concept in depth, offering a comprehensive explanation of how to determine the axis of symmetry in various forms of quadratic expressions, its importance, and practical applications in math and science.
What Is the Equation for Axis of Symmetry?
For any parabola in standard form y=ax2+bx+cy = ax^2 + bx + c, the equation for the axis of symmetry is:
x=−b2ax = \frac{-b}{2a}
The vertex is either the highest or lowest point of the curve, depending on the sign of aa.
Breaking Down the Formula
Let’s understand why the formula makes sense:
- The coefficient aa determines the direction and steepness of the curve.
- Dividing −b-b by 2a2a gives you the x-coordinate where the parabola changes direction—its point of symmetry.
Thus, the equation for the axis of symmetry gives the vertical line that runs through the vertex.
See also: Finding Your Passion: Educational Paths for the Career of Your Dreams
Examples of the Equation in Action
Let’s explore a few examples to illustrate how the formula works.
Example 1:
Given the quadratic equation:
y=2×2+8x+3y = 2x^2 + 8x + 3
Use the formula:
x=−82⋅2=−84=−2x = \frac{-8}{2 \cdot 2} = \frac{-8}{4} = -2
So, the axis of symmetry is the line x=−2x = -2.
Example 2:
Now consider:
y=−3×2+6x−4y = -3x^2 + 6x – 4 x=−62⋅(−3)=−6−6=1x = \frac{-6}{2 \cdot (-3)} = \frac{-6}{-6} = 1
Here, the axis of symmetry is x=1x = 1.
Vertex and Axis of Symmetry
Since the axis of symmetry passes through the vertex, knowing one means you can easily find the other.
Example:
Let’s go back to the first example:
y=2×2+8x+3y = 2x^2 + 8x + 3
We found that x=−2x = -2. Now plug into the original equation:
y=2(−2)2+8(−2)+3=2(4)−16+3=8−16+3=−5y = 2(-2)^2 + 8(-2) + 3 = 2(4) – 16 + 3 = 8 – 16 + 3 = -5
So, the vertex is at (−2,−5)(-2, -5), and the axis of symmetry is x=−2x = -2.
Different Forms of Quadratic Equations
Understanding what is the equation for axis of symmetry depends on the form of the quadratic function. Let’s compare three common forms:
1. Standard Form:
y=ax2+bx+cy = ax^2 + bx + c
Use:
x=−b2ax = \frac{-b}{2a}
2. Vertex Form:
y=a(x−h)2+ky = a(x – h)^2 + k
Here, the axis of symmetry is simply:
x=hx = h
This form gives the vertex directly as (h,k)(h, k), making it even easier to identify the axis.
3. Factored Form:
y=a(x−r1)(x−r2)y = a(x – r_1)(x – r_2)
Where r1r_1 and r2r_2 are the roots.
x=r1+r22x = \frac{r_1 + r_2}{2}
Graphing with the Axis of Symmetry
The axis of symmetry is not just a theoretical line—it’s a powerful graphing tool. Once you know the axis:
- Plot the vertex.
- Draw the axis as a dashed vertical line through the vertex.
- Use symmetry to plot additional points. This method makes drawing a perfect parabola much easier and more accurate.
Real-World Applications
The equation for axis of symmetry has several practical uses in science, engineering, and everyday life.
Projectile Motion
In physics, objects that are thrown or launched follow a parabolic path. The axis of symmetry indicates the time at which the object reaches its highest point.
Engineering and Architecture
Structures like bridges, domes, and suspension cables use parabolic designs. Engineers use the axis of symmetry to maintain balance and uniformity in design.
Economics and Business
Quadratic models are used to determine profit or cost. The axis of symmetry often helps identify optimal pricing strategies by showing the maximum or minimum points of a function.
Common Mistakes to Avoid
When working with the equation for axis of symmetry, watch out for these pitfalls:
- Forgetting the negative sign in -b: This is a frequent error that leads to incorrect values.
- Incorrect values of a or b: Ensure the quadratic is in standard form before applying the formula.
- Misidentifying the vertex: Remember, the vertex lies on the axis, not just near it.
A careful approach and consistent checking can prevent most of these issues.
Conclusion
So, what is the equation for axis of symmetry? In simple terms, it’s a mathematical tool that helps you understand the balance of a quadratic graph. Whether you’re working with the standard form, vertex form, or factored form, the axis of symmetry serves as a foundational concept in algebra.
Mastering this formula not only improves your graphing skills but also deepens your understanding of how quadratic functions behave in both math and the real world.
Whether you’re a student, teacher, or professional, knowing how to find and use the axis of symmetry will enhance your problem-solving skills and analytical thinking.